Team:SUSTech Shenzhen/Genetic Probability Model

Genetic Probability

Model

Genetic probability model

This model describes the process in which we get 2 worm strains with stable genetic traits and the hybrid offspring (with both the preference of blue light and the repulsion to the red light). It was proposed at the beginning of our project, so we were able to decide the frequency of microinjection and estimate how long it would take to get the result. It is a time-consuming step, and to some extent, it determines the whole experiment process.

Fig 2.1 Overview of microinjection Inject plamids in worms gonad by miniMos system.

Fig 2.2 Illustration of screening process for the miniMos System

There are 3 steps to achieve it: Inject plasmid (odr-10::CoCHR::GEM-GECO::mCherry and str-1::Chrimson::GEM-GECO::GFP) through miniMOS system .

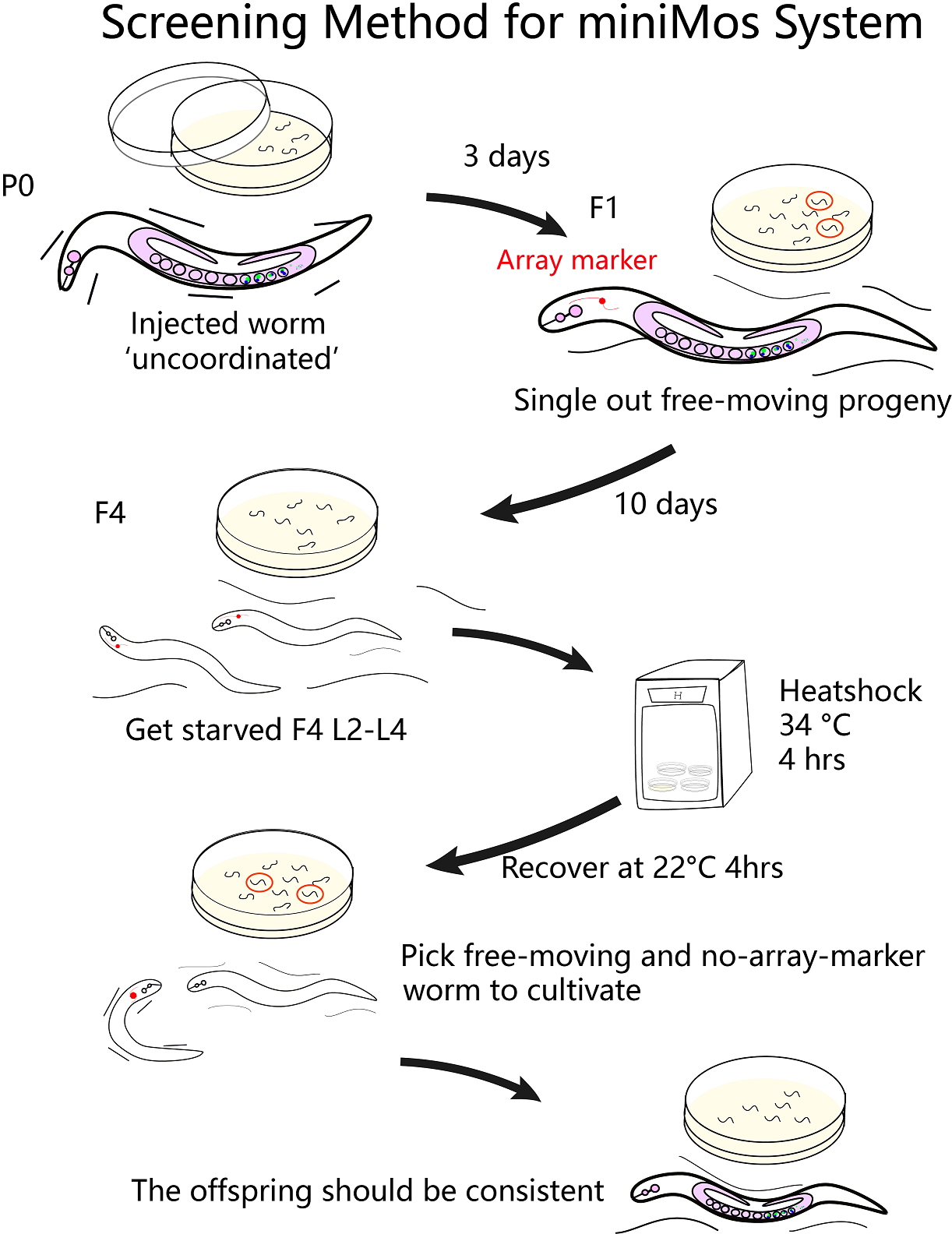
Select the rescued worms using mCherry and GFP.

Mate the 2 strains to get the hybrid offspring of red fluorescence on AWA neuron and green fluorescence on AWB neuron.

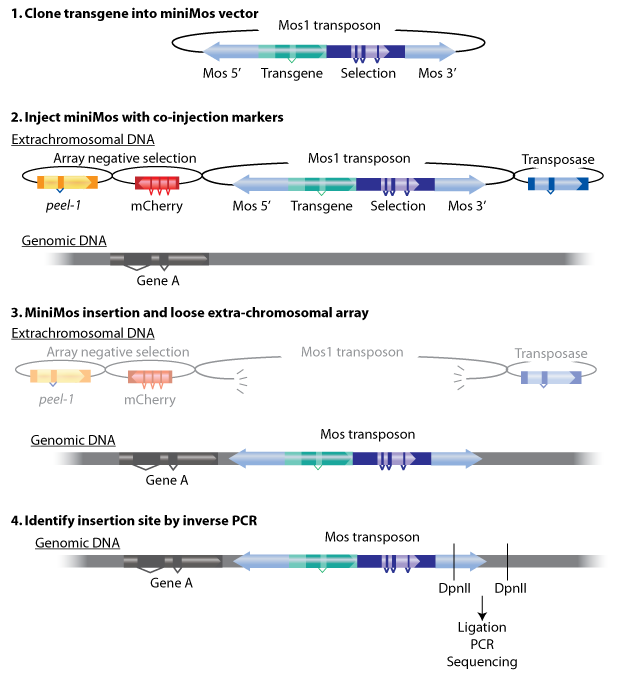
Plasmid injection and selection

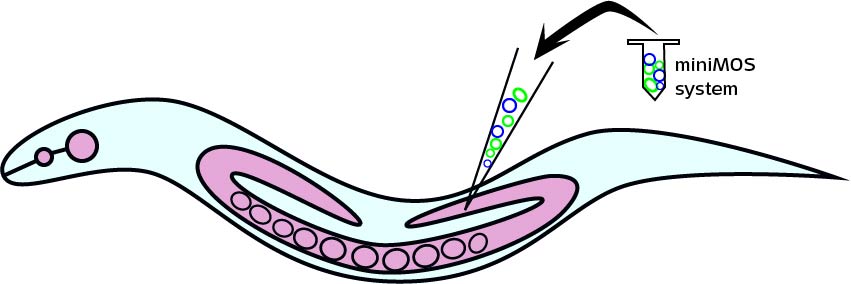
To estimate the total number of worms X that we need to inject, many factors should be considered. It is said in the protocol of miniMos system, “we approximately get insertions from 60% of injected animals and from approximately 10% of all rescued F1 animals. But these numbers will depend greatly on how much practice you have in injecting. ”

Fig 2.3 The MiniMos System

After a long period of practice, our successful rate of injection is around 12%~25%. In calculation, we assume that the rate is 20%. After injecting the gene into its gonad, each worm produces approximately 10 embryos. About 10% of F1 containing the insertion gene can be rescued (The unc-119 gene on the vector plays a key role in ciliary membrane localization of proteins and is required for the establishment or function of the nervous system). Therefore, the number of injected worms we will get from miniMos injection is:

X * 20% * 60%* 10 * 10%

Therefore, to finally get a stain, at the beginning we need to inject at least 9 worms.

After injection and selection, the total time of getting one inserted worms is about 2 weeks.

In fact, we inject totally 40 worms at 2 times to get the odr-10::CoCHR::GEM-GECO::mCherry insertion, and 40 worms to get the str-1::Chrimson::GEM-GECO::GFP. The total time consumption is one and a half months since we injected worms separately.

Mating for stable inheritance

After getting the inserted worms, our next step is to get the hybrid by mating 2 strains. In this step, the probability of obtaining stable inheritance worms depending on the location of inserted gene on the chromosome.

Fig 2.4 Stable inheritance probability

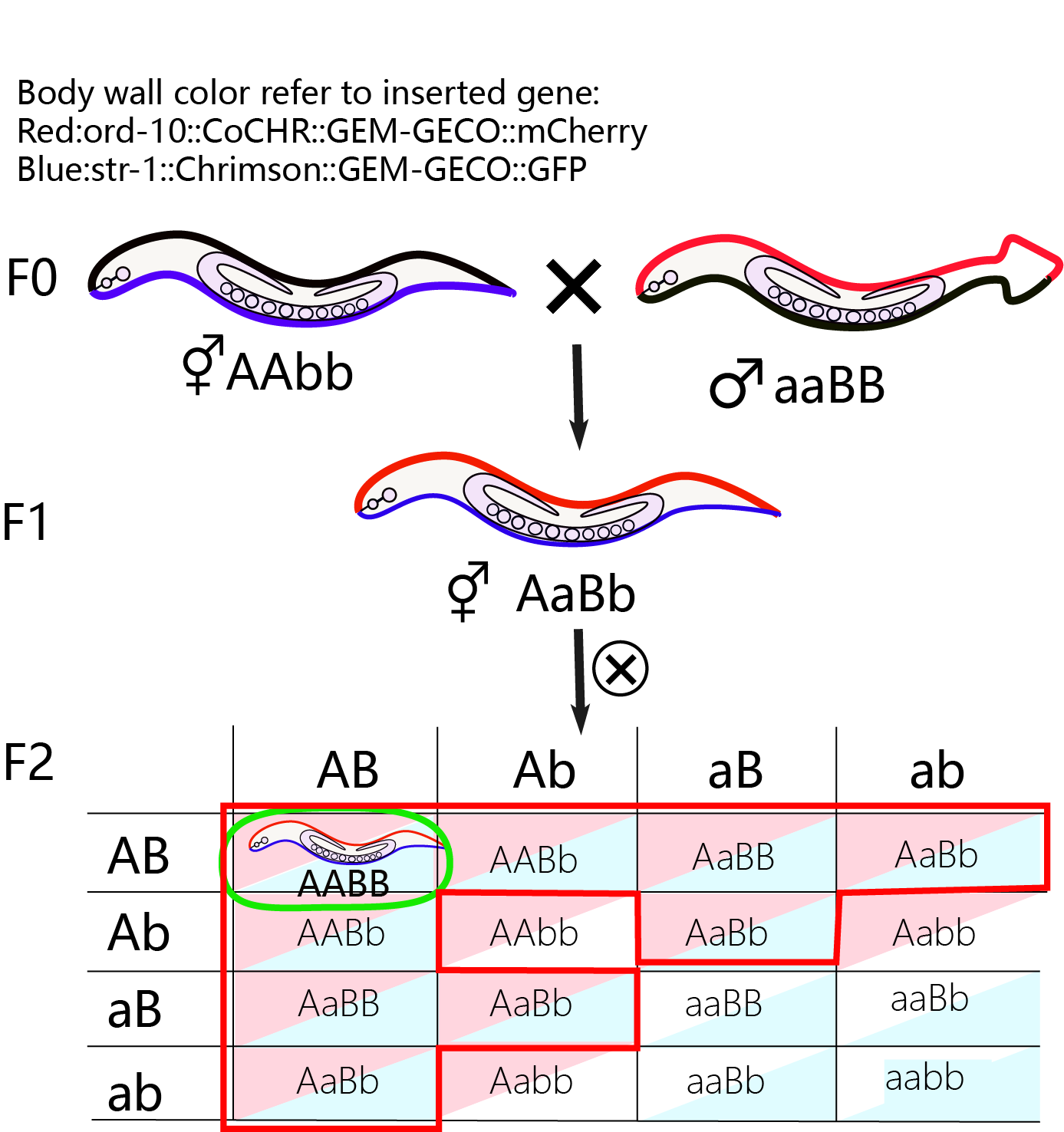
F0: we use ord-10::CoCHR::GEM-GECO::mCherry as male parent and Str-1::Chrimson::GEM-GECO::GFP as female parent.

F1: heterozygote worms with GFP and mcherry.

F2: Four phenotypes of F2, AABB is what we want.

We use pCFJ909 vector as the carrier of insertion gene. It contains mos-1 transposon that can insert the gene on the chromosome randomly. Worms have 6 pair of chromosomes, so the probability of 2 strains with the inserted gene on different chromosomes is 5/6 and the probability of 2 traits are at the same chromosomes is 1/6.

1) Insertions on different chromosomes :

The probability to get stable inheritance is based on the Mendel’s laws. Basically, F1 have both of 2 traits and F2 have trait segregation in . 9/16 of F2 worms contain RFP and GFP in two different neurons. The number of worms with the stable inheritance of 2 traits consist 1/16 of the total number of F2 worms. In this step, the time cost is about 2 weeks.

2) Insertion on single chromosome :

If two insertions located on same chromosome, we still can get worms expressing two light-sensitive proteins by crossing over. However, the time will be much longer than the first circumstance considering the low frequency of chromosome crossing-over. In nature, the probability of crossing over never exceed 50%.If the crossing-over occurs, the probability of the segregation of traits will be 1:1.

Fig 2.5 Chromosome crossing probability

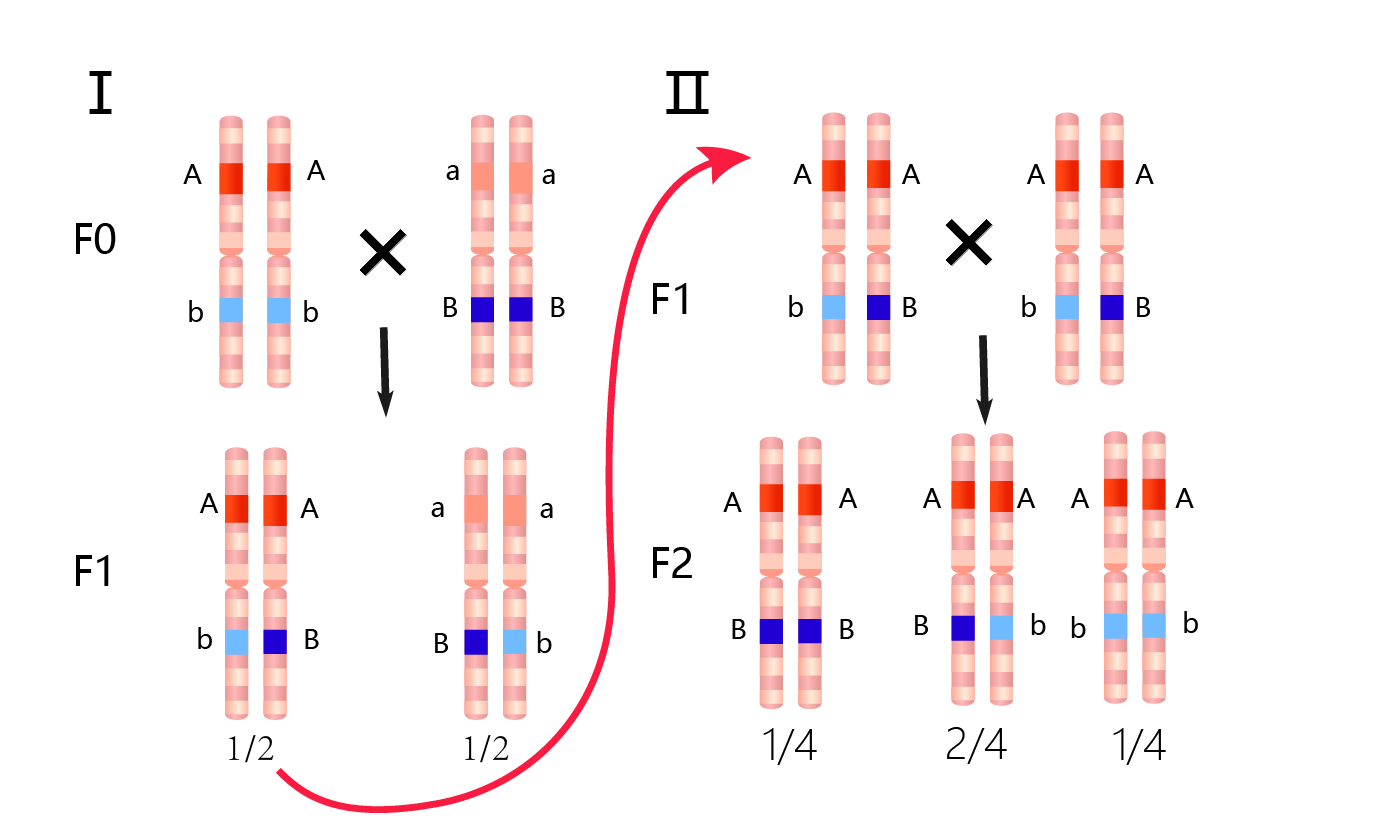
Part I: F0: Homozygote worms obtained via microinjection. Gene A and B are localized on same chromosome. F1: heterozygote offsprings. Part II: Crossing over occurs. F2: Three genotypes obtained.

In our experiment, after successfully getting the 2 strains, the“mapping” method (do the PCR for DNA fragment and “BLAST” it in the C. elegans genebase, or wormbase) is used to determine the locus of inserted gene. The gene, odr-10::CoCHR::GEM-GECO::mCherry is indicated inserted in chromosome I according to the mapping result, but we failed to map the str-1::Chrimson::GEM-GECO::GFP for some unknown reasons. After we did mating experiments, we found that among 40 F2 generation, two of F2 worms showed stable GFP and RFP in their offspring, and others has the offspring with trait segregation. It follows the Mendel’s laws. Therefore, we deduce that odr-10::CoCHR::GEM-GECO::mCherry and str-1::Chrimson::GEM-GECO::GFP are highly possible to be inserted on two different chromosomes.

References

Made by from the elegans.Inc in SUSTech_Shenzhen.

Licensed under CC BY 4.0.

• ©2017 SUSTech_Shenzhen